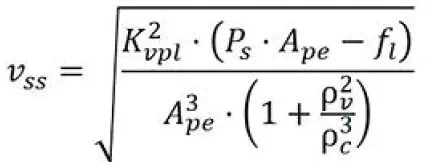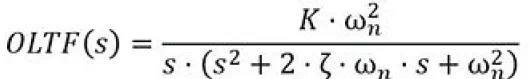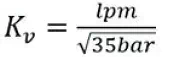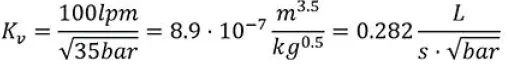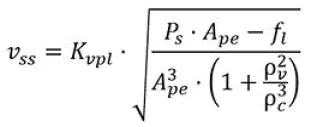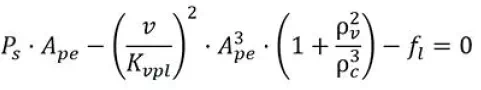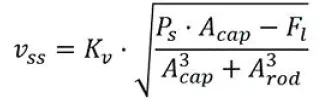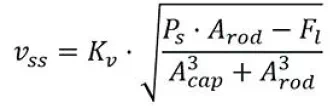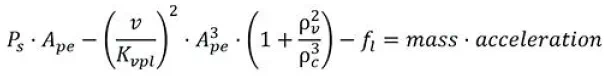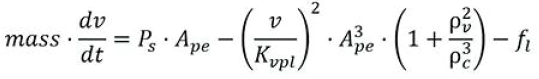译者先说
大多接受过流体力学教育的人都知道,质量守恒是自然界的客观规律,不可压缩液体的流动过程也遵循质量守恒。在流体力学中这个规律用称为连续性方程的数学表达式来表达:Q=A*V,即流体过流截面积与流体速度的乘积为通过的体积流量。这样的知识和理论一直在指引我们前进。而今天,本文带来的是另外一种关于流量(流速)计算的理论即VCCM,其在某些方面刷新了我们对以往知识的认知。
正文
VCCM是什么?
VCCM是Valve control of cylinder motion的缩写,即阀控缸运动控制。该公式由Jack L. Johnson命名,其曾经就职于密尔沃基工学院(Milwaukee School of Engineering)。但是,其最初的起源可追溯至20世纪60年代George Keller在Boeing授课时的内容。
VCCM公式的目的就是表达当伺服阀输入信号100%时,计算执行器所能达到的稳态速度的最大值。
大多数人得到的教育就是速度等于流量除以面积,即V=Q/A,其成立的前提条件就是油缸位置已经移动且执行器上的合力为零不再变化。然而,这种对速度的计算方法是很片面的。公式V=Q/A的存在使人误以为如果减小油缸面积,或者提高供油流量就可以提高速度,然而,事实并非如此!
牛顿在他的三大运动定律里面并没有考虑到流体(流量)特性的作用。
牛顿的第一运动定律(译者注:力是改变物体运动状态的原因,孤立质点保持静止或做匀速直线运动)和第二运动定律(译者注:指出了力的作用效果,力使物体获得加速度)需要扩展以覆盖到液压运动控制。首先,只要负载合力不为零,物体就会一直不断的加速运动。当合力为零的时候,执行器将会达到最大的稳态速度。合力包括使活塞运动的推力,减去油缸另外一腔的液压反作用力,摩擦力和重力等。
VCCM用于阀控缸运动。该术语由Jack Johnson提出,但是该方程本身已经以不同的表达方式存在了很长一段时间了。VCCM方程具有很多用途,但是其最明显的就是当伺服阀全开口的时候决定油缸活塞与负载的最大稳态速度。VCCM可以正确的预知各个方向的稳态速度,而“速度取决于流量(flow makes it go,等式为υ=Q/A)”的方程却做不到。有趣的是,牛顿在他的三大运动定律中并没有涉及到流体运动。
VCCM方程的推导基于油缸活塞两侧的合力。在活塞与负载的合力为零之前,活塞和负载会一直加速运动。如果活塞不再加速,则意味着已经达到稳态速度。液压系统设计者应该熟知VCCM方程及其各种表达式,因为它对优化我们的设计非常有用。
我第一次在Jack Johnson的书里看到的VCCM方程等式为:
此处:
Vss:最大稳态速度
Kvpl:阀功率边(powered land)流量系数(译者注:或者叫进油口)
Ps:供油压力
Ape:油缸活塞功率边的面积(译者注:或者叫油缸进油腔)
fl:负载力,与负载运动方向相反时为负,与负载运动方向相同时为正
ρv:进油口与回油口流量比值
ρc:进油腔有效面积与回油腔有效面积之比
最大的稳态速度发生在阀100%全开时。理解这一点非常重要,因为其决定了开环增益。开环增益用速度与控制输出的百分比来表示,或用(mm/s)/ %来表示。如果稳态速度是500mm/s,则开环增益就是(5mm/s)/ %。正负100%的控制输出也许是±10V,±20mA,或者甚至是4-20mA,此处12mA就是0%的控制输出。
开环增益对于建模很重要。其用在开环传递函数就是:
此处:
OLTF:开环传递函数
K:开环增益
ζ:阻尼系数
L:拉普拉斯算子
ωn:自然频率
如想要对液压缸进行建模,了解其对控制信号的响应,该方程对我们的工程师来说就非常重要。开环增益也用于计算速度前馈增益,其与开环增益相互影响。
因此,如果我们想以250mm/s的速度来移动,而开环增益就是5(mm/s)/ %的话,我们目标速度(250mm/s)除以开环增益,就可以计算得到50%的控制输出。直觉上就会告诉我们如果移动500mm/s就将得到100%的控制输出。
流量系数
阀的流量系数Kvpl如上所述,用于计算稳态速度。如果稳态速度已知,你可以用VCCM方程计算阀的流量系数。阀的流量系数决定了阀的规格大小。伺服阀通常用额定流量,一般用升/分/(35的平方根)。阀通常是在额定压降(70bar)来定义额定流量。然而,压降是发生在两个节流边的-因此70bar必须除以二。
具有额定流量100L/min的阀,在35bar时具有的流量系数是:
你会发现,因为平方根的存在,计算单位显得怪怪的。我想这就是为什么Jack Johnson决定在平方根的下面保留阀流量系数Kvpl 的平方,而不是把阀流量系数移至VCCM方程之前,如下所示。
把单位弄错常常是导致误差的来源。
当分析计算力的时候,其它型式的VCCM方程也许更有用。下面的型式对于计算油缸活塞和阀规格大小非常有用。
VCCM方程的发展
作为液压运动控制器的设计者,活塞和负载在一个方向比另外一个方向移动得更快,对我来说是显然的事情。即使在1980s,我们的液压运动控制器已经把速度前馈增益剥离开来,用于补偿伸出时开环增益和缩回时开环增益之间的差值。如上所述,速度前馈和目标速度可以用于预知控制输出,从而以目标速度运动。
在1990s年代初期,我编了一个程序,使得这种数学符号的运算更为简单。数学符号用于推导类似于上述的方程。我推导出公式用于计算各个方向的前馈。很有必要的是,我重新探索了VCCM方程,并得到了两个公式,一个用于计算伸出,一个用于缩回。我也假设阀是对称的,只是为了让方程更加简单。
Jack Johnson版本的方程似乎显得更为“高贵”一些,因为只有一个方程。然而,因为取决于是伸出还缩回,阀的功率边和回油边的系数是不断变化的。在那时,这些都是计算必须的。如果我知道了所有参数值,我就可以计算最大的稳态速度。
对于我来说,伸出时的方程:
缩回时的方程:
唯一的不同点就在于,供油压力需要乘以流体作用在活塞上的有效作用面积。另外稍微有点区别的是,负载力是正负载还是负负载的考虑,其符号不一样。我的等式里面已经假设在两个方向流量系数都是相等。
然而,我不满足于只是计算稳态速度,开环增益和速度前馈增益。我想知道活塞和负载是如何加速的。因此,我在VCCM方程中增加另外一个表达,用于考虑负载加速时力的变化情况,且我并没有假定在活塞上的合力为零。
这也可以写成:
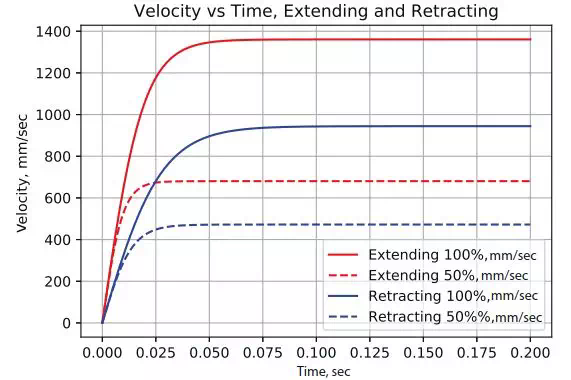
求解这样的非线性微分方程并不是很容易的。其需要数学计算软件工具来协助解决。下面的,将阐述我们在实验室对于液压系统的测试结果。
结论
VCCM方程对于计算最大稳态速度是非常重要的。VCCM方程也可以用于计算油缸和阀的规格。我们已经讨论过,假定油缸活塞面积已知的情况下,如何利用VCCM方程估算阀的规格;其前提是假定我们已经选好了正确规格的油缸尺寸。