如果位置,响应时间和稳定性在系统中至关重要,则设计人员应考虑液压油的体积模量。
大多数人会同意,液压控制系统的性能要求越来越严格。设计人员经常忽略的流体的功能特性之一就是其可压缩性,或者通常称其为体积模量。已经进行了许多实验室测试来测量各种流体的体积弹性模量,因为它会影响系统的性能。
- 什么是体积弹性模量
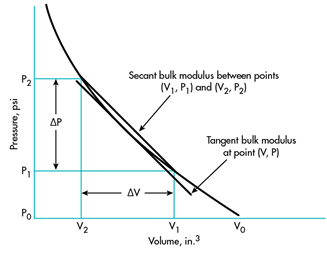
图 1. 流体容积随压力增加而减小
割线体积模量也称为“平均”弹性模量,切线体积模量也称为真实模量
当受到均匀的外部压力时,大多数物质的体积会减少。体积与压力的典型关系图如图1所示。曲线表明
V = f (P,V0, k)
此处: k = 压缩性(通常负值), in.2/lb
P = 压力, psi
V0 =初始容积, in.3
术语“体积弹性模量”通常表示可压缩性的倒数,并且定义了图1中曲线的斜率。陡峭的斜率表示硬的,仅可轻微压缩的流体-一种具有高体积弹性模量的流体。平的坡度表示一种相当可压缩的流体-一种体积模量低的流体。
- 定义体积弹性模量
因为图1中的图不是直线,所以斜率在点与点之间变化。定义斜率或体积弹性模量有两种常用方法:
• 某一点的真实或切线体积弹性模量。在特定点放置与曲线相切的直线边缘会产生切线体积模量。它写为(作为派生词):
Br = dPV/dV.
• 平均或正割体积弹性模量是曲线的任意两个点之间的直线的斜率。那是:
Bs = (P2 – P1)V0/(V1–V2), or Bs = ∆PV0/∆V.
由于在任意两点之间绘制的线显示为弧线的和弦,因此它是割线,因此名称为割线体积弹性模量。
在给出流体体积弹性模量的一些典型值之前,我们必须考虑另一个变量:温度。
温度与体积弹性模量
温度很重要,因为当流体被压缩时,其温度会升高。随着温度升高,流体趋于膨胀,进而产生附加压力。
有两种考虑温度的方法:
• 非常缓慢地压缩流体,以便散发产生的热量。这称为等温(恒温)体积弹性模量。
Brayco 745液压油在3000 psi下的体积弹性模量随温度和空气含量的变化而变化
• 快速压缩流体并测量压力,即使它是由于压缩和热膨胀产生的。这称为绝热体积弹性模量。后者描述了大多数液压应用。因此,本文讨论的大多数体积弹性模量都是绝热的。表1列出了各种流体的一些典型值。
在将表2中的高温和室温下的体积模量值进行比较之后,很容易看出保持流体温度尽可能低的重要性。
预测气液混合物的体积弹性模量
表2中的值是几种气油混合物的有效体积弹性模量。这些通过测试确定,如下所述。使用这些测试结果,开发了一个方便的经验公式来预测(没有测试)其他空气-空气混合物的有效体积模量:
1/Be = 1/B + Va / (Vt × Ba)
此处:
Be 有效体积弹性模量
B 流体体积弹性模量
Va 空气体积
Vt 空气-流体混合(气液混合物)体积
Ba 空气体积弹性模量
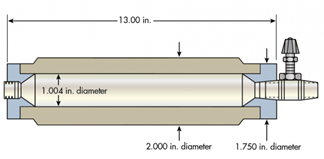
将带有管螺纹孔的厚壁不锈钢焊接钢瓶连接到具有小面积尼龙阀座的长接合针形阀,如图2所示。用手动泵对钢瓶加压。然后使加压流体迅速膨胀到精密玻璃压力计管中。压力计测量了对油缸加压所需的流体量。
在加压的同时,对油缸进行测量以确定其在各种压力下的径向和纵向变形。然后使用材料强度方程式(Timoshenko’s)确定内部挠度,从而获得体积皮重值-从相应的压力计读数中减去该皮重值。测量了夹带或夹带空气为0.125%至1.57%的气油混合物。另外,测量了没有夹带或夹带空气的流体。气油混合物的溶解空气含量(对体积模量值没有影响)保持在2%以下。
空气对体积弹性模量的作用
在使用已发布的体积模量值之前,设计人员应谨慎行事。通常,这些值是通过实验室方法确定的,该方法采取特殊的预防措施,在将流体截留和压缩之前对其进行脱气。
图2.厚壁不锈钢测试筒用于精确测量体积模量。油缸容积为9.45立方英寸。
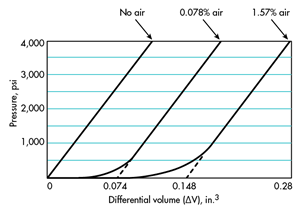
为了说明可能发生的变化,我们在一个厚壁的不锈钢圆筒中测量了绝热体积变化与压力的关系,图2,使用了脱气和充气的流体。图3说明了产生的曲线。它们表明,滞留的空气量将使曲线偏移大约等于当前空气量的值。
图3. 流体中夹带的空气(0.74和0.148立方英寸)降低了流体的体积模量。
如可以直观地推断出的那样,曲线的直线部分直到流体中夹带的空气量被压缩才开始。压缩空气后,所有曲线的斜率都相同。如果从0 psig测量,则可以看出,随着空气含量的变化,绝热(正割)体积模量值将有很大差异。从表2中的绝热本体模块的值中可以看出这一点。(对观察到的测试值进行了调整,以适应因圆柱体膨胀而产生的不同体积,然后计算出本体模量的值。)
泵和执行器的体积损失
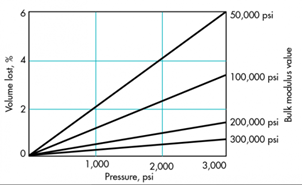
图4.体积模量值较高的流体的体积减小较少
泵的输出或主从执行器的位置关系随所用流体的体积模量而变化。图4示出了体积损失百分数与压力和体积模量的关系。对于泵,输出中的百分比体积损失被视为马力损失。对于主从执行器,体积损失被视为从属冲程的损失。
准备图4时使用的公式是:
∆V/V0 × 100% = 100 × P/ B
停止移动负载
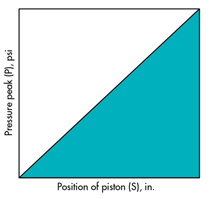
图5.由于流体可压缩性而吸收(浪费)的功。阴影面积乘以活塞面积等于吸收的功。
如果油缸以均匀的速度移动负载(至油缸的流量恒定),则当阀流突然关闭时,负载具有必须由流体和系统吸收的动量。如果阀位于下游,则随着能量的吸收,流体压力将从标称值上升到某个峰值压力,图5。假设刚性缸体和管路以及压力线性上升,则流体的体积模量将确定峰值压力。曲线下的面积乘以活塞面积即表示功:
W = F × S
W = ½ ( P × A) × ∆s
完成的功(吸收的能量)等于移动负载的动能EK,即:
W = EK = (½ W/g) × v2
此处
W = 做功
F = 作用在负载上的力
s = 移动距离
EK =动能
g = 重力加速度,恒值
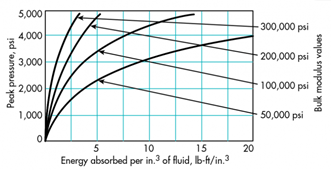
图6体积模量值较高的流体吸收的能量较少,活塞的过冲量也较小(定位精度更高)
把功的单位从英寸转化到英尺:
功 (ft-lb) = 1/24 P (psi) × A× ∆s
因为A × ∆s = ∆V = ∆P × V0/B, 则EK = (∆P)2 × V0 /24B.
此处V0 = 执行器与管道所困的容积.
图6显示了各种体积弹性模量下每立方英寸流体的峰值压力与能量(ft-lb)的关系。可以看出,对于特定的最大压力,流体越硬,吸收的能量越少,超调量也越小。致动器体积的增加会增加其能量吸收和过冲。
- 快速的负载逆转
由于大多数流体都是可压缩的,因此在油缸的活塞移动负载之前,必须先对执行器中的流体进行压缩。换句话说,在执行任何有用功之前,必须将等于压缩体积的流体量添加到执行器中。由于此过程无法完成有用功,因此会浪费掉无用功。
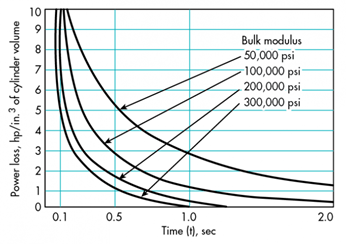
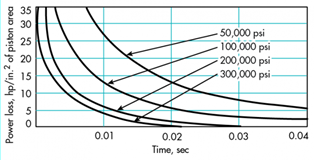
图7. 对于1立方英寸的油缸容积在3000pis压力下的功率损失
WL = F × s = ∆P+ × AP × si = ∆P × A ×∆s
此处:
∆P+ = 压力上升
AP = 柱塞面积
si = 位移增加值
因此: WL = ∆P × ∆V
但是∆V = ∆P × V0/B, so因此: WL= ∆P2 × B × V0
t:除以时间t获得损失的功率
WL = ∆P2 × V0 /(B × t × 6600)
由于功率在较高的压力范围内变得很重要,因此让我们检查一个典型的3000 psi系统,即∆P = 3000 psi。
PL = 1363 V0/(B × t)
此处: PL= 损失的马力, hp
图8. 1平方英寸的活塞面积和10英寸的行程在3000 psi时的功率损耗。在短时间间隔内
图7显示了执行器体积为1立方英寸容积,在各种体积弹性模量时的功率损耗与时间的关系图。功率损耗随执行器尺寸的增加而增加,响应时间减少。图8说明了各种体积弹性模量的损耗功率与响应速率的关系。
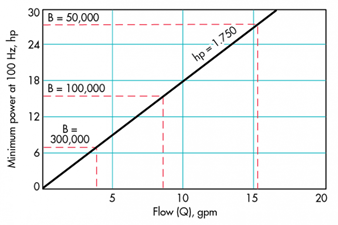
在我们考虑平均执行器之前,功率损耗可能看起来相对较小。如果我们假设其体积模量为200,000psi,响应速度为100Hz,行程为10英寸,则每平方英寸撞锤面积的损失为6.75hp。图9将功率损耗与可用的总系统功率相关联。例如,一个可以提供6.75hp功率的3000psi,3.8gpm的系统无法使用1平方英寸的推杆移动100Hz的负载,因为所有功率都将用于压缩流体。
液压系统的共振
弹簧-质量组合的固有频率为:
f = (1/2π) (kg/W)1/2
此处: f = 功率, Hz
W = 重量, lb
k = 弹簧刚度,lb/in.
要将其等同于液压系统,我们只需要用弹性模量代替体积模量即可。因此,低模量也降低了系统的固有频率。例如,如果1%的空气含量将流体的体积模量改变了50%,则其固有频率将降低30%。这大大降低了系统的稳定性。
- 为什么体积弹性模量很重要
图9.以100 Hz驱动系统(移动执行器)所需的最小功率
从前面的讨论中,应该清楚的是,流体的体积模量的绝对值会严重影响与位置,功率水平,响应时间和稳定性有关的系统性能。
控制体积模量的两个主要因素是流体温度和夹带空气含量。例如,表2显示,仅将Brayco 745液压油的温度升高100°F便会将其体积模量降低至其室温值的61%。表2还表明,按体积计引入1%的空气会将体积模量降低至其室温值的55%。如果这两个条件同时发生,则净效果将使体积模量降低67%。
总而言之,鉴于当今对增加功率和响应时间的要求,因此,设计人员应该比以往更多地关注体积模量。